An Introduction
Most communication systems (human speech, sonar, microwave, radio, co-ax, fiber optics, twisted pair etc) are simply described in terms of:![]()
- Transmitter power
- Transmission path degradation
- Receiver sensitivity (power)
It is therefore quite natural that communications engineers should use a system of units and measurements that enables these three elements to be easily defined and calculated.
Note that transmitter power and receiver sensitivity are absolute power levels (eg Watts or dBm), whereas the transmission path degradation is a relative value (eg dB or % reduction), which is generally independent of the actual power level involved. Path degradation may involve a combination of factors, such as attenuation and dispersion. For this discussion, we will just refer to signal attenuation, or loss.
The universal measurement system adopted for this purpose is the Decibel, which is a logarithmic unit. The decibel unit allows system parameters to be easily calculated by addition and subtraction, rather than multiplication and division.
Example
How this makes calculations simple is shown in an example of a fiber optic transmission system:
Absolute power levels in this example are expressed in dBm and generally refer to input and output power levels. The ‘m’ refers to the reference level used, in this case mW (milli Watts). The reference level used for optical systems is usually 1 mW, since the absolute transmitter power is often approximately this power level. So a value of 0 dBm decibel is 1 mW.
| Emitter power |
-4 dBm
|
| Receiver sensitivity |
-27 dBm
|
Allowable degradation, or loss budget: -27 -(-4) = -23 dB
Signal attenuation in this example is defined in dB units and generally refers to transmission path losses (Lossy transmission path)
| Signal decrease of 1st fiber section |
7.3 dB
|
| Signal decrease of 2nd section |
4.8 dB
|
| Signal decrease of 3rd section |
6.9 dB
|
So the calculated transmission degradation of the complete link is 7.3 + 4.8 + 6.9 = 19 dB (dB loss definition is negative, eg -s19 dB)
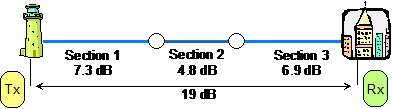
Figure A1-1
| Therefore spare system margin |
-19 – (-23) = 4 dB
|
Note that in this example, although the total transmission impairment is 19 dB, the spare system margin is only 4 dB. Since measuring uncertainties can easily add up to over 1 dB ( eg 1.9 dB in this case, with 3 sections ), spare system margin can easily be confused with measurement uncertainty ( eg 4 ± 1.9 dB = 2.1 – 5.9 dB margin after uncertainty allowance ). Hence the importance of making measurements as accurate as possible.
The definition of the dBm unit is:
|
dB = 10 log ( P1/P2 ) where |
For absolute measurements, the reference power P2 is usually defined as 1 milliwatt, hence dBm. Therefore 0 dBm = 1 mW:
AKA: ‘decibel dB definition’, ‘dBm power definition’, or ‘decibel definition’
| dBm Power unit | mW power unit | dBm Power unit | mW power unit |
| +20 | 100 mW | -30 | 1 µW |
| +10 | 10 mW | -40 | 100 nW |
| 0 | 1 mW | -50 | 10 nW |
| -10 | 100 µW | -60 | 1 nW |
| -20 | 10 µW | -70 | 100 pW |
For relative dB measurements, P2 is arbitrarily defined by the user:
| dB | Relative value | dB | Relative value | |||
| +20 | x100 | 102 | -30 | /1,000 | 10-3 | |
| +10 | x 10 | 101 | -40 | /10,000 | 10-4 | |
| 0 | x 1 | 100 | -50 | /100,000 | 10-5 | |
| -10 | /10 | 10-1 | -60 | /1 million | 10-6 | |
| -20 | /100 | 10-2 | -70 | /10 million | 10-7 | |
The dBm decibels unit also has the following useful attributes:
- It reduces large numbers to a convenient size ( eg -70 dB = 1/10,000,000 ).
- It offers constant resolution for a given number of decimal places, which improves calculation confidence. 0.1 dB gives 2.3 % resolution. 0.01 dB gives 0.23 % resolution.
- It is a universal unit that an engineer can apply to any communications link.
How much dBm / dB measurement resolution do I need?
Meters are available with resolution ranging from 0.1 to 0.001 dB / dBm, with cost differences to match:
0.001 dBm / dB resolution may be occasionally useful in carefully controlled laboratory conditions, however even in this situation, it’s difficult to make use of this much resolution.
0.1 dB resolution may not be enough. This performance is often adequate to measure absolute power levels, but can not reliably measure connector or splice loss, since the measurement uncertainty involved will be in excess of ± 0.14 dB ( eg ± 1 digit, over 2 measurements ). This is purely due to display limitations, and assumes otherwise perfect performance.
0.01 dB ( 0.23% ) resolution is ideal for most work on fibre systems. It is for this reason that Kingfisher instruments generally provide a resolution of 0.01 dB.
Calculating dBm measurement uncertainty
To calculate the total measurement uncertainty, the following general rules can be used:
Linear uncertainty can be added using the usual RMS method. For example the total of 3 uncertainties of 4 %, 3 % and 2 %, = ?(42 + 32 + 22 ) = 5.4 % ( not 9 % ).
However dBm / dB uncertainty values must be converted to linear values and then averaged using the above method.
In practice, this inconvenience can often be avoided by use of a “decibel math” rule of thumb as follows:
f the 2nd highest logarithmic value is less than 80% of the highest value, the uncertainty is approximated to the largest value.
If the 2nd highest value is over 80% of the highest value, multiply the highest value by 1.4 for the combined figure.
In practical situations, one or two uncertainty figures tend to dominate the others. Here are some examples:
Three different uncertainty values of 0.3 dB, 0.2 dB, 0.1 dB, give a combined uncertainty of 0.35 dB. The error in ignoring the lower values is only 0.05 dB.
Two similar uncertainty values of 0.3 and 0.29 dB, give a combined uncertainty of 0.39 dB. The approximated figure is 0.42 dB, out by only 0.03 dB.
Five different uncertainty values of 0.4, 0.2, 0.1, ,0.09, 0.05 dB give a combined uncertainty of 0.42 dB. This is within 0.02 dB of the approximated figure of 0.4 dB.
dB Averaging
Within the telecommunications industry, a links attenuation is commonly calculated by averaging a bi-directional measurement. There are various reasons given for this, but the most important practical reasons are that this method eliminates meter calibration errors and minimises the effects of source drift. This is of course simple stuff, however the hidden flaw is that it is mathematically incorrect for logarithmic or dB units to be treated this way. The correct method is to first convert to linear, then average and finally convert back to dB. Further reading on this topic can be found in Kingfisher Application Note A14, Improving Attenuation Measurement Accuracy
Electro – Optic Conversion:
Optical signals are usually converted to an electric current, which is then measured as a voltage across a resistor (in a trans-impedance amplifier).
The electrical power dissipated by the resistor goes up with the square of the voltage.
So the optical receiver power also goes up with the square of the optical signal.
So when working in volts, the relationship is defined as: dB = 20 log (V1/V2)
Where
V1 = measured voltage
V2 = reference voltage ( eg 1 mV )